Capital Asset Pricing Model (CAPM)

Capital Asset Pricing Model (CAPM)

Sukrit Mittal Franklin Templeton Investments

Outline

  1. Why CAPM?
  2. Assumptions and market setting
  3. From portfolio choice to equilibrium
  4. Derivation of CAPM
  5. Security Market Line (SML)
  6. Systematic vs idiosyncratic risk
  7. Characteristic line
  8. Empirical interpretation and limits
  9. Exercises

1. Why CAPM?

Up to now we solved investor problems.

CAPM answers a different question:

How are assets priced in equilibrium?

This is not about optimal portfolios.

It is about consistency across the entire market.

The fundamental question: If all investors are mean-variance optimizers, what must expected returns look like?

What CAPM Is—and Is Not

CAPM is: A model of how risk translates into return

CAPM is not: A trading strategy

It is a benchmark.

Historical Context

Developed independently by:

Sharpe won the Nobel Prize in Economics (1990) for this work.

The model revolutionized finance by providing a testable theory of expected returns.

2. Market Setting and Assumptions

We assume:

  1. Mean–variance optimization: All investors choose portfolios based only on expected return and variance

  2. Homogeneous expectations: All investors agree on:

    • Expected returns \(\mu\)
    • Covariance matrix \(\Sigma\)
    • Risk-free rate \(R_f\)

  3. Perfect capital markets:

    • No transaction costs
    • No taxes
    • Assets are infinitely divisible
    • All assets are marketable and liquid

  4. Single-period horizon: All investors have the same investment horizon

  5. Risk-free borrowing and lending: Investors can lend or borrow unlimited amounts at rate \(R_f\)

These assumptions are strong.

Why These Assumptions?

What each assumption enables:

Relaxing these assumptions leads to extensions and alternative models.

But understanding CAPM requires accepting them first.

Critique of Assumptions

Homogeneous expectations is the most controversial:

Perfect markets:

The question is not whether assumptions are true.

The question is whether the model is useful despite them.

3. From Portfolio Choice to Equilibrium

From Lecture 07, we know:

In equilibrium:

The risky portfolio held by everyone must be the market portfolio.

Why? Market clearing.

This is the critical step.

The Market Portfolio

The market portfolio \(M\) contains:

Definition:

\[ w_i^M = \frac{\text{Market value of asset } i}{\text{Total market value of all assets}} \]

Examples:

No asset can escape the market.

If it exists, it is priced.

Equilibrium Condition

In equilibrium, two conditions must hold:

  1. Optimality: Each investor holds an optimal portfolio given prices

  2. Market clearing: Total demand = Total supply for every asset

Combining these:

\[ \text{Aggregate holdings} = \text{Market portfolio} \]

Since everyone holds the tangency portfolio, it must equal the market portfolio.

This pins down expected returns.

4. Risk Decomposition

Consider an asset \(i\) with return \(R_i\).

Decompose its risk relative to the market \(R_M\).

Only part of this risk matters, rest is diversifiable noise.

Total Risk Decomposition

Any asset's return can be written as:

\[ R_i = \mathbb{E}[R_i] + \beta_i(R_M - \mathbb{E}[R_M]) + \varepsilon_i \]

Where:

Total variance:

\[ \text{Var}(R_i) = \beta_i^2 \text{Var}(R_M) + \text{Var}(\varepsilon_i) \]

Beta: Measuring Systematic Risk

Define beta:

\[ \beta_i = \frac{\text{Cov}(R_i, R_M)}{\text{Var}(R_M)} \]

Beta measures:

Sensitivity to market movements.

Interpretation:

This is the only risk investors are paid for.

Why? Because idiosyncratic risk can be diversified away.

5. Derivation of CAPM

Consider the market portfolio \(M\).

For any asset \(i\):

Otherwise, \(M\) would not be optimal.

This restriction pins down expected returns.

Derivation via Marginal Contribution to Risk

Consider a portfolio with weight \(\alpha\) in asset \(i\) and \((1-\alpha)\) in the market portfolio \(M\).

Portfolio return:

\[ R_p(\alpha) = \alpha R_i + (1-\alpha) R_M \]

Portfolio variance:

\[ \sigma_p^2(\alpha) = \alpha^2 \sigma_i^2 + (1-\alpha)^2 \sigma_M^2 + 2\alpha(1-\alpha) \text{Cov}(R_i, R_M) \]

At \(\alpha = 0\) (pure market portfolio), the Sharpe ratio must be maximized.

First-order condition for maximum Sharpe ratio:

\[ \frac{d}{d\alpha}\left[\frac{\mathbb{E}[R_p(\alpha)] - R_f}{\sigma_p(\alpha)}\right]\Bigg|_{\alpha=0} = 0 \]

Derivation (continued)

The Sharpe ratio of the mixed portfolio is:

\[ S(\alpha) = \frac{\mathbb{E}[R_p(\alpha)] - R_f}{\sigma_p(\alpha)} \]

For \(M\) to be optimal, the derivative with respect to \(\alpha\) must be zero at \(\alpha = 0\).

Step 1: Derivative of expected return

\[ \frac{d\mathbb{E}[R_p]}{d\alpha} = \mathbb{E}[R_i] - \mathbb{E}[R_M] \]

Step 2: Derivative of variance

\[ \frac{d\sigma_p^2}{d\alpha} = 2\alpha \sigma_i^2 + 2(1-2\alpha)\sigma_M^2 - 2(1-2\alpha)\text{Cov}(R_i, R_M)\]

At \(\alpha = 0\):

\[ \frac{d\sigma_p^2}{d\alpha}\Bigg|_{\alpha=0} = 2[\text{Cov}(R_i, R_M) - \sigma_M^2] \]

Step 3: Derivative of standard deviation

\[ \frac{d\sigma_p}{d\alpha}\Bigg|_{\alpha=0} = \frac{1}{\sigma_M}[\text{Cov}(R_i, R_M) - \sigma_M^2] \]

Step 4: Apply quotient rule to Sharpe ratio

\[ \frac{dS}{d\alpha} = \frac{\frac{d\mathbb{E}[R_p]}{d\alpha} \cdot \sigma_p - (\mathbb{E}[R_p] - R_f) \cdot \frac{d\sigma_p}{d\alpha}}{\sigma_p^2} \]

At \(\alpha = 0\), set numerator to zero:

\[ [\mathbb{E}[R_i] - \mathbb{E}[R_M]] \sigma_M = [\mathbb{E}[R_M] - R_f] \cdot \frac{\text{Cov}(R_i, R_M) - \sigma_M^2}{\sigma_M} \]

Step 5: Simplify

CAPM Equation

Rearranging:

\[ \mathbb{E}[R_i] - \mathbb{E}[R_M] = \frac{\mathbb{E}[R_M] - R_f}{\sigma_M^2}[\text{Cov}(R_i, R_M) - \sigma_M^2] \]

For the market portfolio itself, \(\text{Cov}(R_M, R_M) = \sigma_M^2\), so this holds with equality.

For any other asset \(i\):

\[ \mathbb{E}[R_i] = \mathbb{E}[R_M] + \frac{\mathbb{E}[R_M] - R_f}{\sigma_M^2}[\text{Cov}(R_i, R_M) - \sigma_M^2] \]

Rearranging:

\[ \mathbb{E}[R_i] = R_f + \frac{\text{Cov}(R_i, R_M)}{\sigma_M^2}[\mathbb{E}[R_M] - R_f] \]

Using \(\beta_i = \frac{\text{Cov}(R_i, R_M)}{\sigma_M^2}\):

\[ \boxed{\mathbb{E}[R_i] - R_f = \beta_i\big( \mathbb{E}[R_M] - R_f \big)} \]

This is the CAPM equation.

Alternative Derivation: Equilibrium Pricing

Equilibrium condition: The market portfolio is the tangency portfolio.

From Lecture 07, the tangency portfolio satisfies:

\[ w^M \propto \Sigma^{-1}(\mu - R_f \mathbf{1}) \]

This means:

\[ \mu - R_f \mathbf{1} \propto \Sigma w^M \]

The \(i\)-th component:

\[ \mu_i - R_f \propto \sum_j \Sigma_{ij} w_j^M = \text{Cov}(R_i, R_M) \]

The proportionality constant is the same for all assets:

\[ \mu_i - R_f = \lambda \cdot \text{Cov}(R_i, R_M) \]

For the market portfolio itself:

\[ \mu_M - R_f = \lambda \cdot \text{Var}(R_M) \]

Therefore:

\[ \lambda = \frac{\mu_M - R_f}{\sigma_M^2} \]

Substituting back:

\[ \mathbb{E}[R_i] - R_f = \frac{\mu_M - R_f}{\sigma_M^2} \cdot \text{Cov}(R_i, R_M) = \beta_i(\mu_M - R_f) \]

Same result, different path.

6. Security Market Line (SML)

Plot expected return against beta.

The CAPM predicts a straight line:

\[ \mathbb{E}[R_i] = R_f + \beta_i (\mathbb{E}[R_M] - R_f) \]

This line is the Security Market Line (SML).

Key points on the SML:

Graphical Representation:

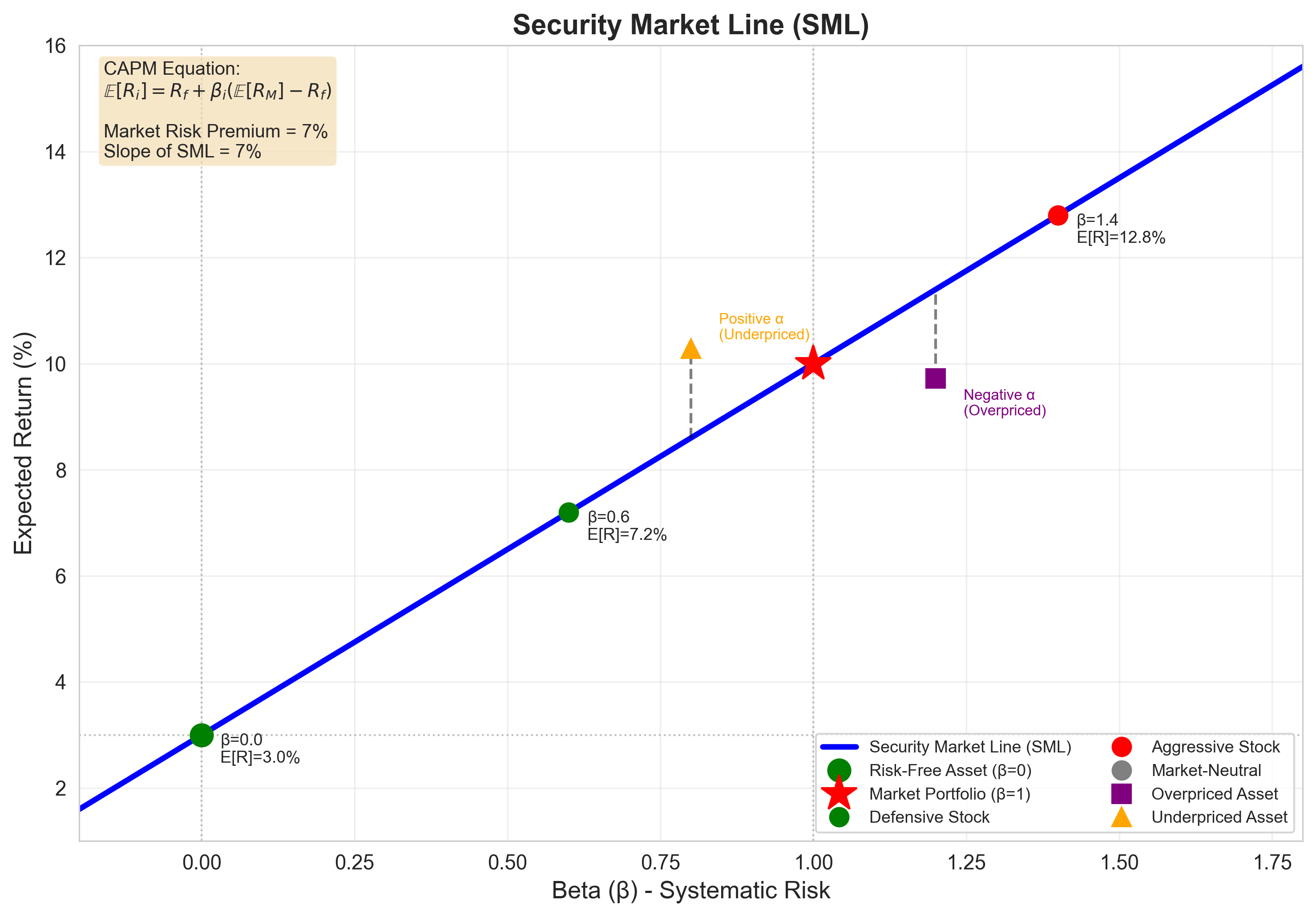
Security Market Line

Figure: The Security Market Line shows the linear relationship between beta and expected return predicted by CAPM. Assets above the line are underpriced (positive alpha), while those below are overpriced (negative alpha).

Interpretation of the SML

Components:

Economic interpretation:

\[ \text{Expected excess return} = \beta \times \text{Market risk premium} \]

Asset pricing implications:

In theory.

Numerical Example: Using the SML

Suppose:

Asset A: \(\beta_A = 0.8\) (defensive)

\[ \mathbb{E}[R_A] = 0.03 + 0.8(0.10 - 0.03) = 0.03 + 0.056 = 8.6\% \]

Asset B: \(\beta_B = 1.5\) (aggressive)

\[ \mathbb{E}[R_B] = 0.03 + 1.5(0.10 - 0.03) = 0.03 + 0.105 = 13.5\% \]

Asset C: \(\beta_C = 1.2\), observed return = \(15\%\)

CAPM prediction:

\[ \mathbb{E}[R_C] = 0.03 + 1.2(0.07) = 11.4\% \]

Actual return (15%) > CAPM prediction (11.4%)

Interpretation: Asset C is underpriced or has positive alpha.

7. Systematic vs Idiosyncratic Risk

Total risk decomposes into:

Diversification eliminates only the latter.

Markets pay only for what cannot be diversified.

Mathematical Decomposition

Recall the risk decomposition:

\[ R_i = \mathbb{E}[R_i] + \beta_i(R_M - \mathbb{E}[R_M]) + \varepsilon_i \]

Taking variance:

\[ \text{Var}(R_i) = \beta_i^2 \text{Var}(R_M) + \text{Var}(\varepsilon_i) \]

R-squared: Fraction of variance explained by the market:

\[ R^2 = \frac{\beta_i^2 \text{Var}(R_M)}{\text{Var}(R_i)} \]

Why Only Systematic Risk Is Priced

Key insight: In a well-diversified portfolio, idiosyncratic risks cancel out.

For a portfolio of \(n\) assets with equal weights:

\[ R_p = \frac{1}{n}\sum_{i=1}^n R_i = \mathbb{E}[R_p] + \beta_p(R_M - \mathbb{E}[R_M]) + \frac{1}{n}\sum_{i=1}^n \varepsilon_i \]

Where \(\beta_p = \frac{1}{n}\sum_{i=1}^n \beta_i\).

Variance of idiosyncratic component:

If \(\varepsilon_i\) are uncorrelated with average variance \(\bar{\sigma}_\varepsilon^2\):

\[ \text{Var}\left(\frac{1}{n}\sum_{i=1}^n \varepsilon_i\right) = \frac{\bar{\sigma}_\varepsilon^2}{n} \to 0 \text{ as } n \to \infty \]

Conclusion: Large portfolios eliminate idiosyncratic risk.

Since investors can diversify at zero cost, they won't pay a premium for bearing idiosyncratic risk.

Visual Decomposition:

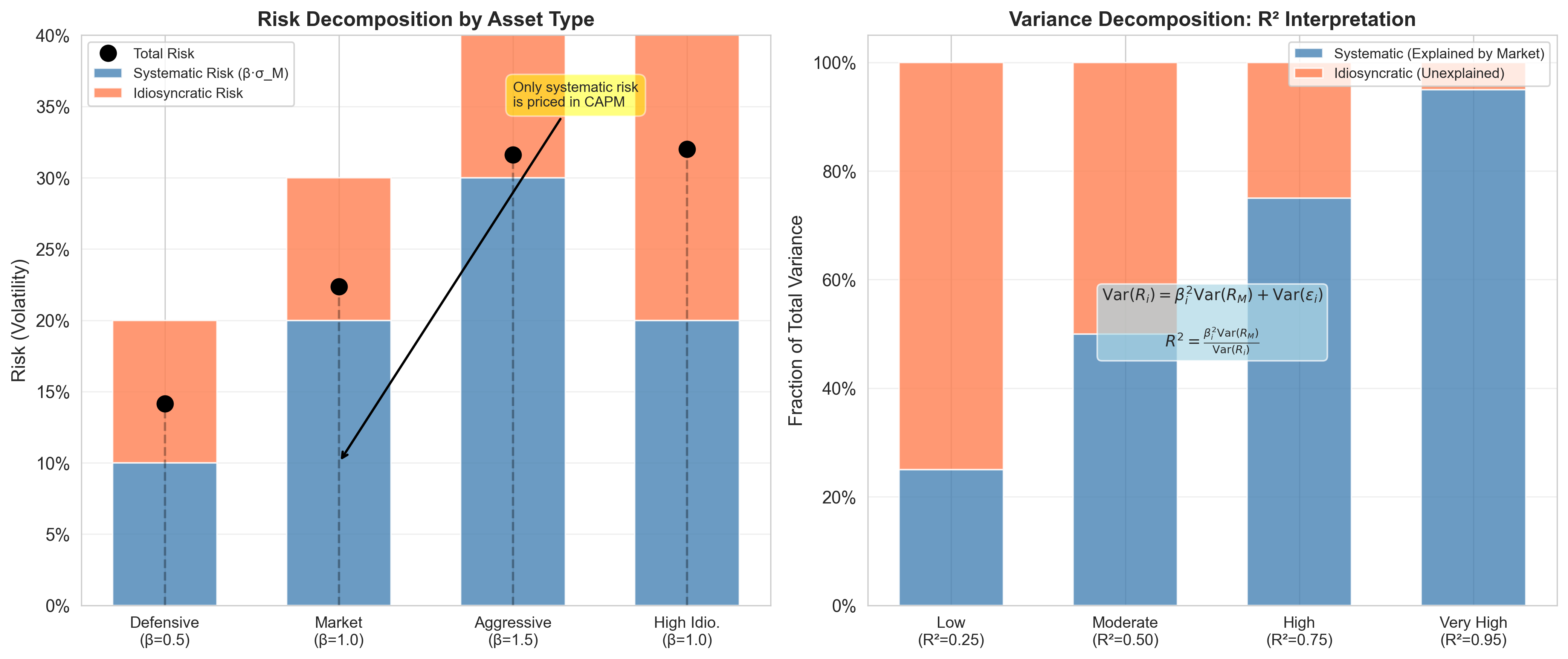
Risk Decomposition

Figure: (Left) Risk decomposition for different asset types showing systematic and idiosyncratic components. (Right) R² interpretation showing the fraction of variance explained by the market.

Numerical Example: Diversification

Consider 50 stocks, each with:

Individual stock variance:

\[ \text{Var}(R_i) = (1.2)^2(0.04) + 0.04 = 0.0576 + 0.04 = 0.0976 \]

Standard deviation: \(\sigma_i = 31.2\%\)

Equally-weighted portfolio variance:

\[ \text{Var}(R_p) = (1.2)^2(0.04) + \frac{0.04}{50} = 0.0576 + 0.0008 = 0.0584 \]

Standard deviation: \(\sigma_p = 24.2\%\)

Risk reduction: From 31.2% to 24.2% (22% reduction)

8. Characteristic Line

The characteristic line relates an asset's excess return to the market's excess return:

\[ R_i - R_f = \alpha_i + \beta_i (R_M - R_f) + \varepsilon_i \]

This is a regression equation.

Components:

Assumptions:

This is not just a theoretical construct — it's how we estimate beta in practice.

Graphical Representation:

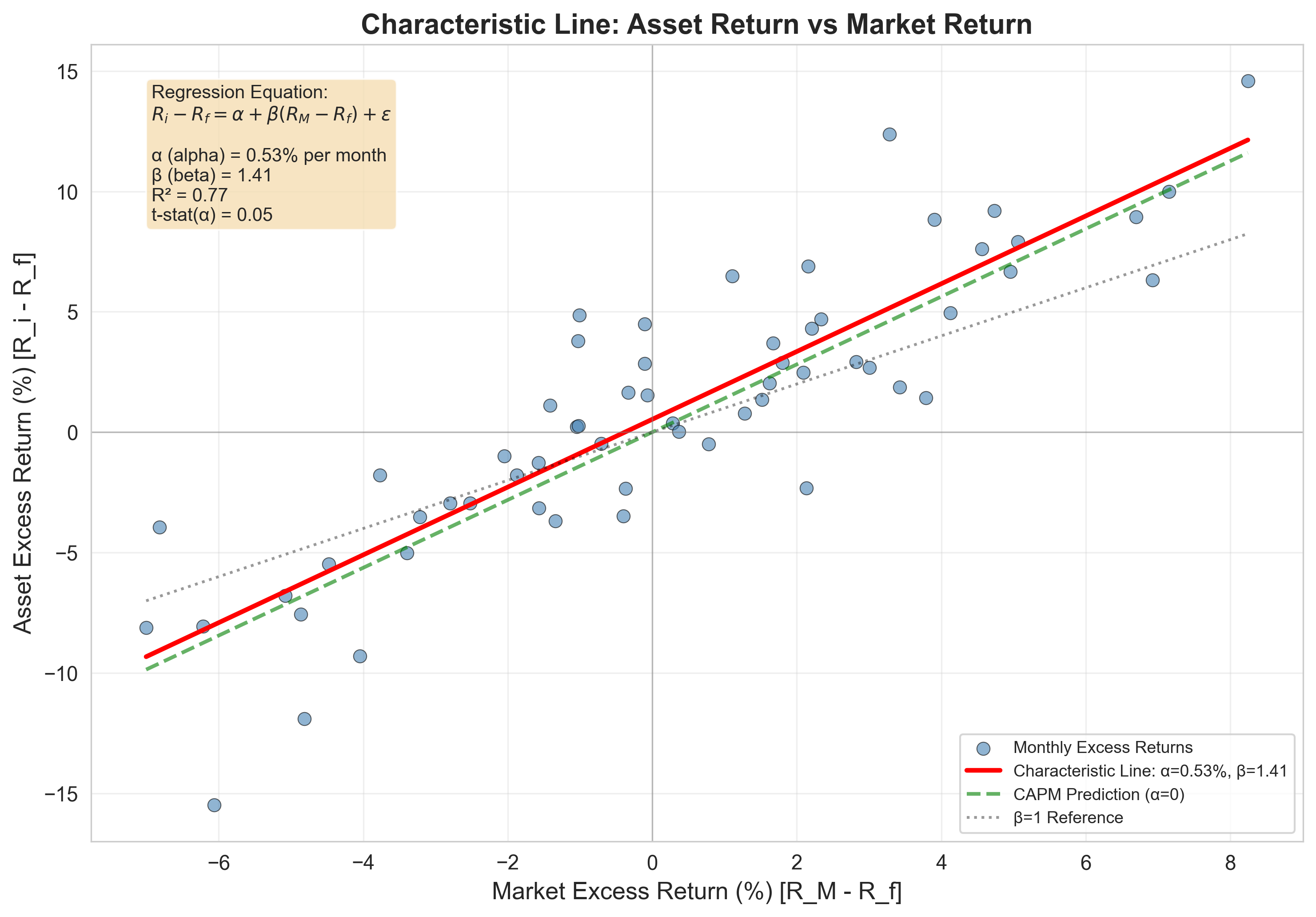
Characteristic Line

Figure: The characteristic line shows the regression of asset excess returns against market excess returns. The slope is beta, and the intercept is alpha. Positive alpha indicates outperformance relative to CAPM predictions.

Interpretation of Parameters

Beta (\(\beta_i\)):

Alpha (\(\alpha_i\)):

Residual (\(\varepsilon_i\)):

In CAPM:

\[ \alpha_i = 0 \]

Nonzero alpha is a claim.

Extraordinary claims require extraordinary evidence.

Estimating Beta: Time-Series Regression

Data: Historical returns for asset \(i\) and market \(M\) over \(T\) periods

Regression:

\[ r_{i,t} - r_{f,t} = \alpha_i + \beta_i(r_{M,t} - r_{f,t}) + \varepsilon_{i,t} \]

for \(t = 1, 2, \ldots, T\)

Ordinary Least Squares (OLS) estimate:

\[ \hat{\beta}_i = \frac{\sum_{t=1}^T (r_{i,t} - \bar{r}_i)(r_{M,t} - \bar{r}_M)}{\sum_{t=1}^T (r_{M,t} - \bar{r}_M)^2} \]

Standard error:

\[ \text{SE}(\hat{\beta}_i) = \frac{\hat{\sigma}_\varepsilon}{\sqrt{\sum_{t=1}^T (r_{M,t} - \bar{r}_M)^2}} \]

Where \(\hat{\sigma}_\varepsilon\) is the standard deviation of residuals.

Beta Estimation Examples:

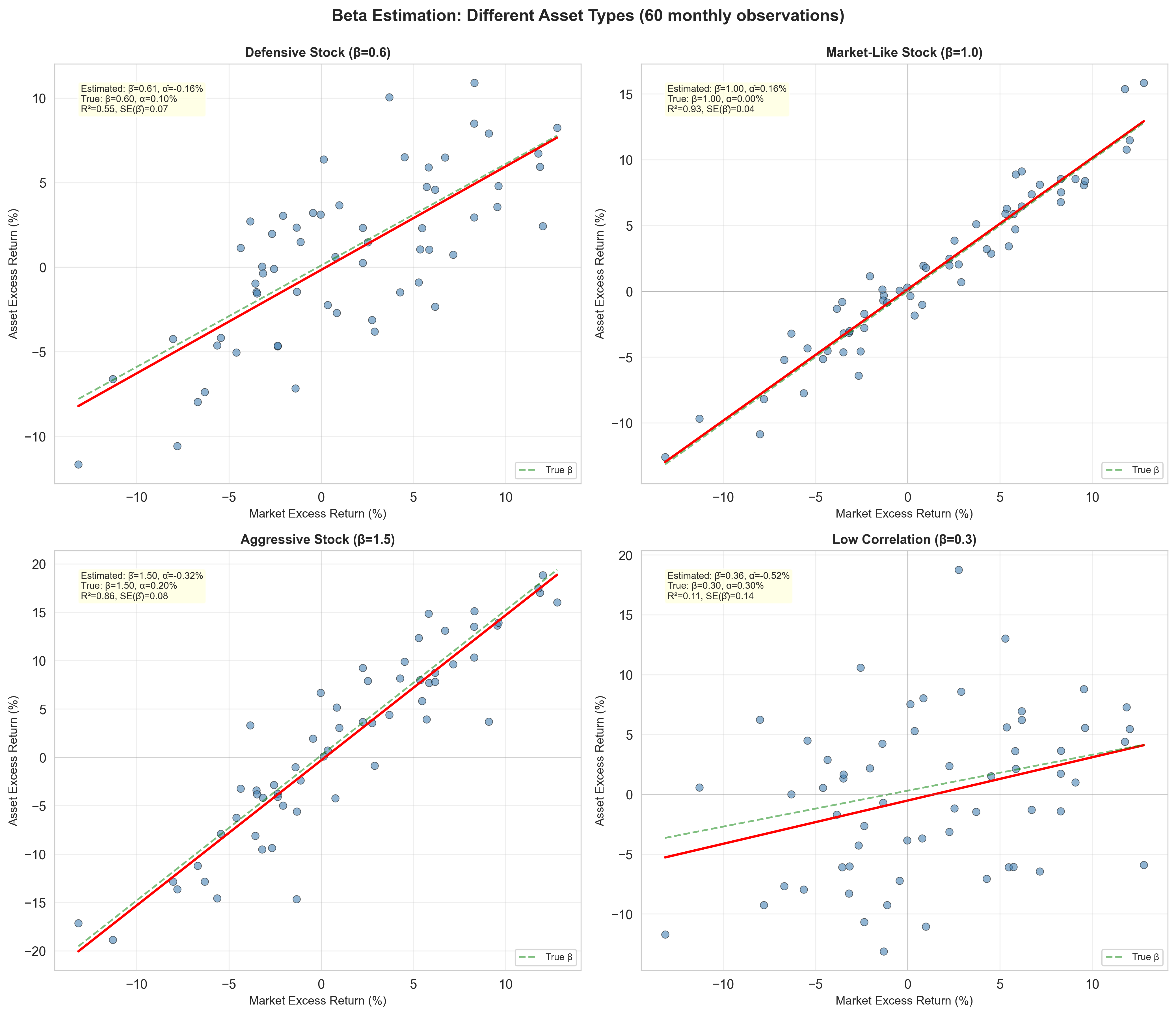
Beta Estimation

Figure: Beta estimation for different asset types using time-series regression. Each panel shows 60 monthly observations with the fitted characteristic line. Note how R² varies with the strength of market correlation.

Numerical Example: Estimating Beta

Suppose we have 60 monthly returns for Stock XYZ and the S&P 500.

Regression results:

\[ r_{\text{XYZ},t} - r_{f,t} = 0.005 + 1.35(r_{M,t} - r_{f,t}) + \varepsilon_t \]

Interpretation:

CAPM prediction: With \(R_f = 2\%\) and \(\mathbb{E}[R_M] = 9\%\):

\[ \mathbb{E}[R_{\text{XYZ}}] = 0.02 + 1.35(0.09 - 0.02) = 11.45\% \]

If alpha persists, expected return would be: \(11.45\% + 6\% = 17.45\%\)

9. Empirical Reality

CAPM is elegant.

Reality is less cooperative.

Empirically:

But CAPM survives as a benchmark.

Bad models die.

Useful models endure.

Empirical Tests of CAPM

Classic tests:

  1. Black, Jensen, Scholes (1972): Found that low-beta stocks earn higher returns than CAPM predicts

  2. Fama-French (1992): Size and book-to-market ratio explain returns better than beta alone

  3. Roll's critique (1977): CAPM is untestable because the true market portfolio is unobservable

Key empirical findings:

Why CAPM Fails Empirically

Violated assumptions:

  1. Not all investors are mean-variance optimizers

    • Some use heuristics, others are constrained

  2. Heterogeneous expectations

    • Investors disagree about expected returns

  3. Market frictions matter

    • Transaction costs, taxes, short-sale constraints

  4. The market portfolio is unobservable

    • S&P 500 ≠ true market portfolio
    • Should include bonds, real estate, human capital, etc.

  5. Time-varying risk premiums

    • Market risk premium changes with economic conditions

Despite failures, CAPM remains useful:

Extensions and Alternatives

Multi-factor models:

Consumption CAPM (CCAPM):

Intertemporal CAPM (ICAPM):

Arbitrage Pricing Theory (APT):

Behavioral models:

CAPM opened the door.

Others walked through.

10. Exercises

Exercise 1: Basic CAPM Calculation

Given:

Tasks:

  1. Calculate the expected return for Stock A using CAPM
  2. Calculate the expected return for Stock B using CAPM
  3. Which stock has higher expected return? Higher risk? Explain.
  4. If Stock A's actual expected return is 14%, what is its alpha?

Exercise 2: Beta Estimation

You have the following data for Stock XYZ over 5 years:

Year Stock Return Market Return Risk-Free Rate
1 12% 8% 2%
2 -5% -3% 2%
3 18% 12% 2%
4 8% 6% 2%
5 15% 10% 2%

Tasks:

  1. Calculate excess returns for both stock and market
  2. Estimate beta using the formula: \(\hat{\beta} = \frac{\text{Cov}(r_i - r_f, r_M - r_f)}{\text{Var}(r_M - r_f)}\)
  3. Estimate alpha from the regression intercept
  4. What is the R-squared of this relationship?
  5. Discuss limitations of using only 5 years of data

Exercise 3: Security Market Line

An asset lies persistently above the SML.

List and explain three possible reasons:

  1. Reason 1: _____
  2. Reason 2: _____
  3. Reason 3: _____

For each reason, discuss:

Exercise 4: Risk Decomposition

A stock has:

Tasks:

  1. Calculate the systematic risk component: \(\beta_i^2 \sigma_M^2\)
  2. Calculate the idiosyncratic risk component: \(\text{Var}(\varepsilon_i)\)
  3. What is the R-squared? Interpret this value.
  4. If you hold 30 of these stocks (equally weighted, uncorrelated idiosyncratic risk), what is the portfolio's total variance?
  5. How much of the risk is eliminated by diversification?

Exercise 5: Portfolio Beta

You have a portfolio with three stocks:

Stock Weight Beta
A 30% 0.8
B 50% 1.3
C 20% 1.6

Given \(R_f = 4\%\) and \(\mathbb{E}[R_M] = 12\%\):

Tasks:

  1. Calculate the portfolio beta: \(\beta_p = \sum_i w_i \beta_i\)
  2. Calculate the expected return of the portfolio using CAPM
  3. Verify this matches the weighted average of individual expected returns
  4. If you want to achieve \(\beta_p = 1.0\), how should you adjust the weights?

Exercise 6: CAPM and Cost of Capital

A company is considering a new project with the following characteristics:

Tasks:

  1. Calculate the required rate of return using CAPM
  2. The project requires an initial investment of $10M and is expected to generate $12M in one year. Should the company accept the project?
  3. What is the NPV of the project?
  4. What beta would make the project break-even (NPV = 0)?

Final Takeaways

Key insight: CAPM is wrong, but useful.

It provides a disciplined way to think about risk and return.

All models are simplifications.

Good models clarify thinking even when they fail empirically.

Next lecture: We move beyond simple models to utility theory and risk measurement via Value-at-Risk (VaR).

The journey from portfolio theory to risk management.